Optimal periodic resource allocation in reactive dynamical systems: application to Microalgal production
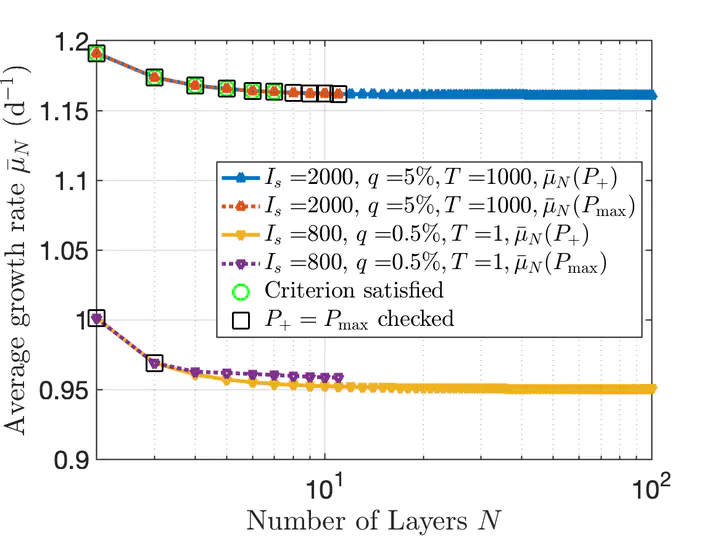 Quality of the approximation and the criterion
Quality of the approximation and the criterionAbstract
In this paper we focus on a periodic resource allocation problem applied on a dynamical system which comes from a biological system. More precisely, we consider a system with $N$ resources and $N$ activities, each activity use the allocated resource to evolve up to a given time $T > 0$ where a control (represented by a given permutation) will be applied on the system to re-allocate the resources. The goal is to find the optimal control strategies which optimize the cost or the benefit of the system. This problem can be illustrated by an industrial biological application, namely the optimization of a mixing strategy to enhance the growth rate in a microalgal raceway system. A mixing device, such as a paddle wheel, is considered to control the rearrangement of the depth of the algae cultures hence the light perceived at each lap. We prove that if the dynamics of the system is periodic, then the period corresponds to one re-allocation whatever the order of the involved permutation matrix is. A nonlinear optimization problem for one re-allocation process is then introduced. Since $N!$ permutations need to be tested in the general case, it can be numerically solved only for a limited number of $N$. To overcome this difficulty, we introduce a second optimization problem which provides a suboptimal solution of the initial problem, but whose solution can be determined explicitly. A sufficient condition to characterize cases where the two problems have the same solution is given. Some numerical experiments are performed to assess the benefit of optimal strategies in various settings.