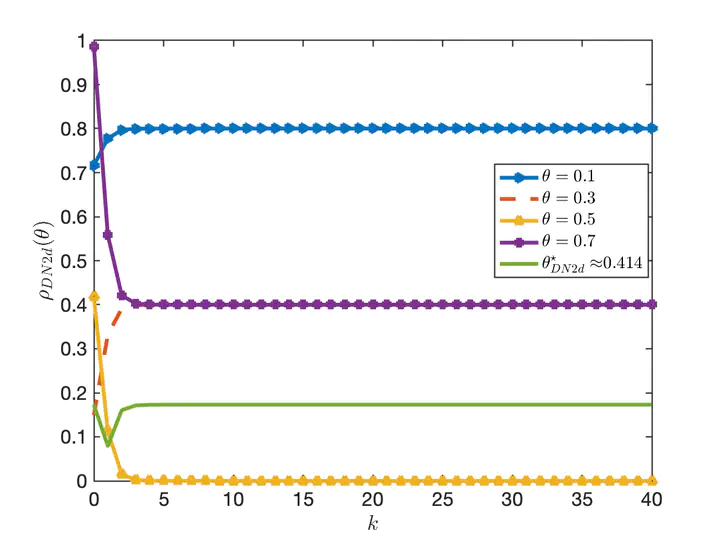
 Convergence factors in 2D for the DN algorithm
Convergence factors in 2D for the DN algorithmAbstract
We present the Dirichlet-Neumann (DN) and Neumann-Neumann (NN) methods applied to the optimal control problems arising from elliptic partial differential equations (PDEs) under the $H^{-1}$ regularization. We use the Lagrange multiplier approach to derive a forward-backward optimality system with the $L^2$ regularization, and a singular perturbed Poisson equation with the $H^{-1}$ regularization. The $H^{-1}$ regularization thus avoids solving a coupled bi-Laplacian problem, yet the solutions are less regular. The singular perturbed Poisson equation is then solved by using the DN and NN methods, and a detailed analysis is given both in the one-dimensional and two-dimensional case. Finally, we provide some numerical experiments with conclusions.